Imports and exports respond to regional prices (PRI) relative to those elsewhere. As a measure of prices elsewhere, IFs uses a world average price (WP), weighted by regional gross production and adjusted by the exchange rate (EXRATE).

The computation uses lagged prices because at this point the recursive equation system has not yet computed current prices.

Exports are responsive to both changes in production and changes in prices via respective elasticities. On the production side we begin by computing an export base (XBASE). It is initial exports (XS) plus some portion (XKAV) of growth in production, represented by potential gross sectoral production (ZSP). Representing a moving average of incremental production that is exported helps maintain global balance and stable behavior in long-term forecasting. The exported portion is modified over time in response to two elasticities. The first is a fairly standard elasticity of exports with income/production growth ( elasxinc ). The second is an export shift parameter that one would normally use to represent scenarios about export promotion or constraint.

Given the export base, export capacity (XC) responds to the difference between local and global prices using an elasticity of trade with prices ( elastrpr ). In addition we use two parameters (first order and second order) to pursue dynamically a global trade balance over time ( elprx1 and elprx2 ). You may wish more detail on the adjustment mechanism.

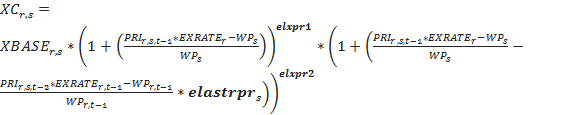
Import capacities or demands (MD) are almost exactly analogous. Whereas exports are tied to production, however, imports are tied to a demand base (DBASE) made up of final demands plus gross sectoral production potential (ZSP).

Imports are responsive to both changes in income and changes in prices and respective elasticities. We use the demand base as the basis for the income term. Specifically, we create a basic import level (MBASE) that grows with the demand base, responsive to an income elasticity parameter for imports ( elasminc ).

A moving average for imports (MKAV) as a portion of changes in the demand base helps maintain global balance and stable behavior over the long-term.

Given this income responsive import base, regional prices relative to global ones (again with first and second order terms), an elasticity of imports with prices ( elastrpr ), and parameters for dynamic change of imports ( elprm1 and elprm2 ) largely determine import demands. One last factor, however, is a domestic protection multiplier ( protecm ), which can cause the import price (MPRIC) to rise or fall relative to the world price.

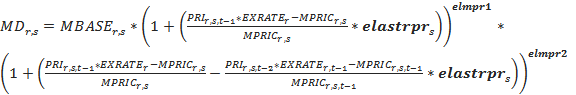
where

World export capacity (WXC) and world import demand (WMD) are simply sums across regions.

These will always be somewhat different. Actual world trade (WT) is the average of the two.

We are now able to compute actual sectoral exports (XS) and imports (MS), normalizing the capacity for exports and the demand for imports to the actual world trade.

We can now update the moving average export (XKAV) and import (MKAV) propensities for the next cycle. This requires historical weights ( xhw and mhw ) for exports (XHW) and imports (MHW).

The above equations are necessary only for three of the five economic sectors. The agriculture and energy models compute trade in those sectors separately. Given the computation of sectoral exports and imports for all sectors (in this or other models), it is possible to compute total exports (X) and imports (M).

IFs also computes these in a "relative-priced adjusted" form, multiplying the real sectoral values by global prices. Why is this important? If, for example, a country were highly dependent on energy exports and the price of energy (from the energy model) doubled relative to other prices, failure to adjust trade for prices would understand the country’s trade balance. It is the relative price-adjusted trade that is taken to the international financial calculations.

A purely optional adjustment to the relative price adjusted import and export levels is available for the model user who wishes to examine the hypothetical impact of changes in the terms of trade. The terms of trade parameter ( termtrm ) is a multiplier with a normal value of 1.0. Higher values shift the terms of trade in the favor of Southern or less-developed regions (those with initial GDP per capita less than an amount, such as $5,000, specified by nsdiv ) and lower values favor Northern regions. The determination of North and South by initial GDP per capita and the fixing of those categories is important. 

The adjustment to regional exports and imports for hypothetical terms-of-trade change can result in a failure of exports and imports to sum across regions to the same global total. At this point IFs thus normalizes regional exports and imports to a total value for world trade equal to the average of the current sums of exports and imports across regions.

Given final values for regional exports and imports it is possible to compute regional trade balances (TRADEBAL), using relative-price adjusted exports and imports.